CS336: Language Modeling from Scratch

Stanford / Spring 2025

学习笔记整理：杨桂淼 课程主页：https://stanford-cs336.github.io/spring2025/

Goal

This course is designed to provide students with a comprehensive understanding of language models by walking them through the entire process of developing their own. Drawing inspiration from operating systems courses that create an entire operating system from scratch, we will lead students through every aspect of language model creation, including data collection and cleaning for pre-training, transformer model construction, model training, and evaluation before deployment.

Tokenization

Tokenizers是将字符串和整数序列之间进行相互转换，四类主要的分词器：character_tokenizer、byte_tokenizer、word_tokenizer、bpe_tokenizer。

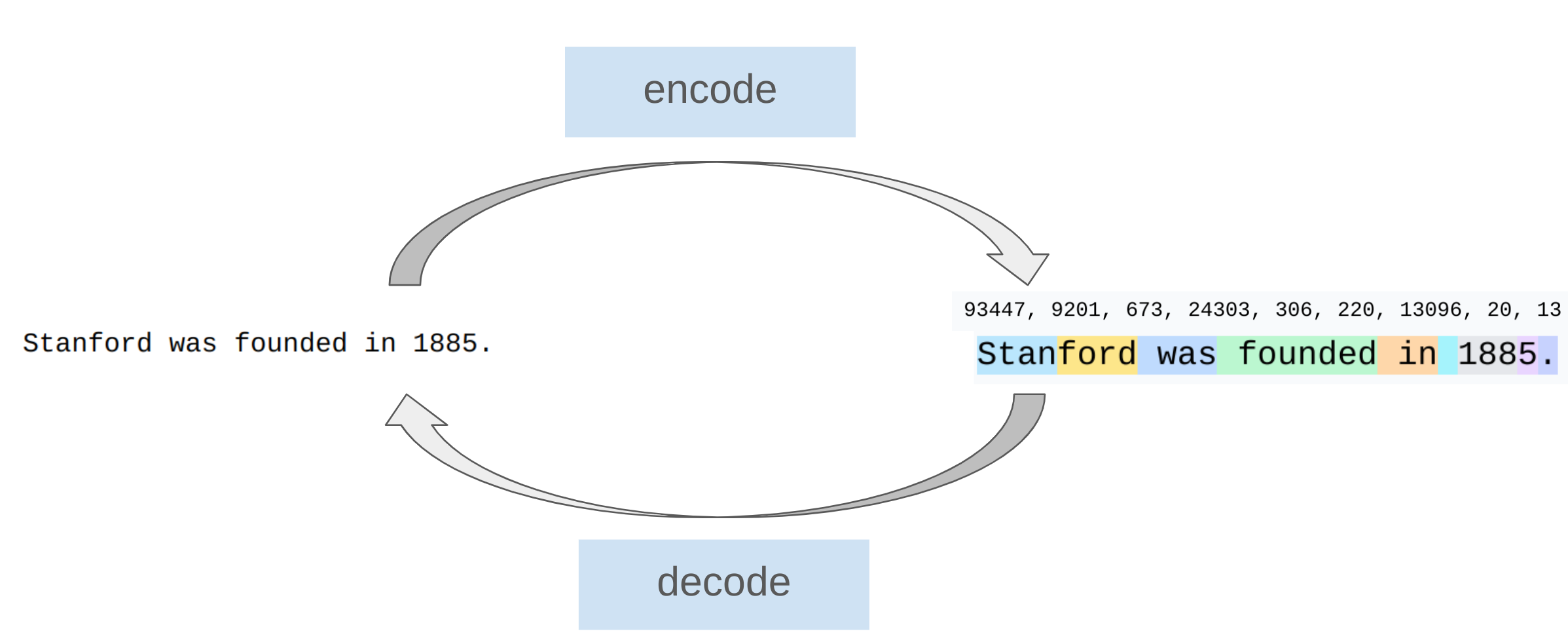
character_tokenizer：每个字符可以通过ord函数完成字符到ASCII码(Unicode)的相互转换。但是带来的问题就是构成的词表非常大，许多字符生僻少用导致词汇使用效率低。

byte_tokenizer：Unicode字符可以被表示为一个使用0-255整数表示的字节序列。但是由于一个字节只能被256个整数所表示，这就造成了经过Tokenization后的序列长度会变得非常长。

word_tokenizer：NLP领域内常用的方法是将字符串分割为单词，利用正则表达式构建分词器，将基于分词器得到的segments映射为整数，构建出每个segment的整数映射。但是存在的问题是单词的数量巨大，无法提供固定的词汇量；训练期间未使用过的新词会被标记为UNK，扰乱困惑度计算。

💡联想语言模型的输出：LLM的输出本质上就是在一个大的词表上预测单词的概率分布，如果词表非常大，那么计算了可想而知是非常恐怖的，而且也会影响token的预测。上面介绍的三种Tokenization都各有特点，但是也都存在致命的缺点。LLM基于上述编码的劣势，最终选择采用BPE算法作为模型的Tokenization方法。

Byte Pair Encoding

BPE算法是在1994年发表的“A New Algorithm for Data Compression”提出的一种新型数据压缩算法。核心思想就是将序列中常见的一对相邻的数据单元替换为数据中没有出现过的新单元，反复迭代直至满足终止条件。

bpe_tokenizer：基本思路是常见的字符序列被单个token表示，罕见的序列被多个tokens表示。

BPE的基本计算路程如下所示：

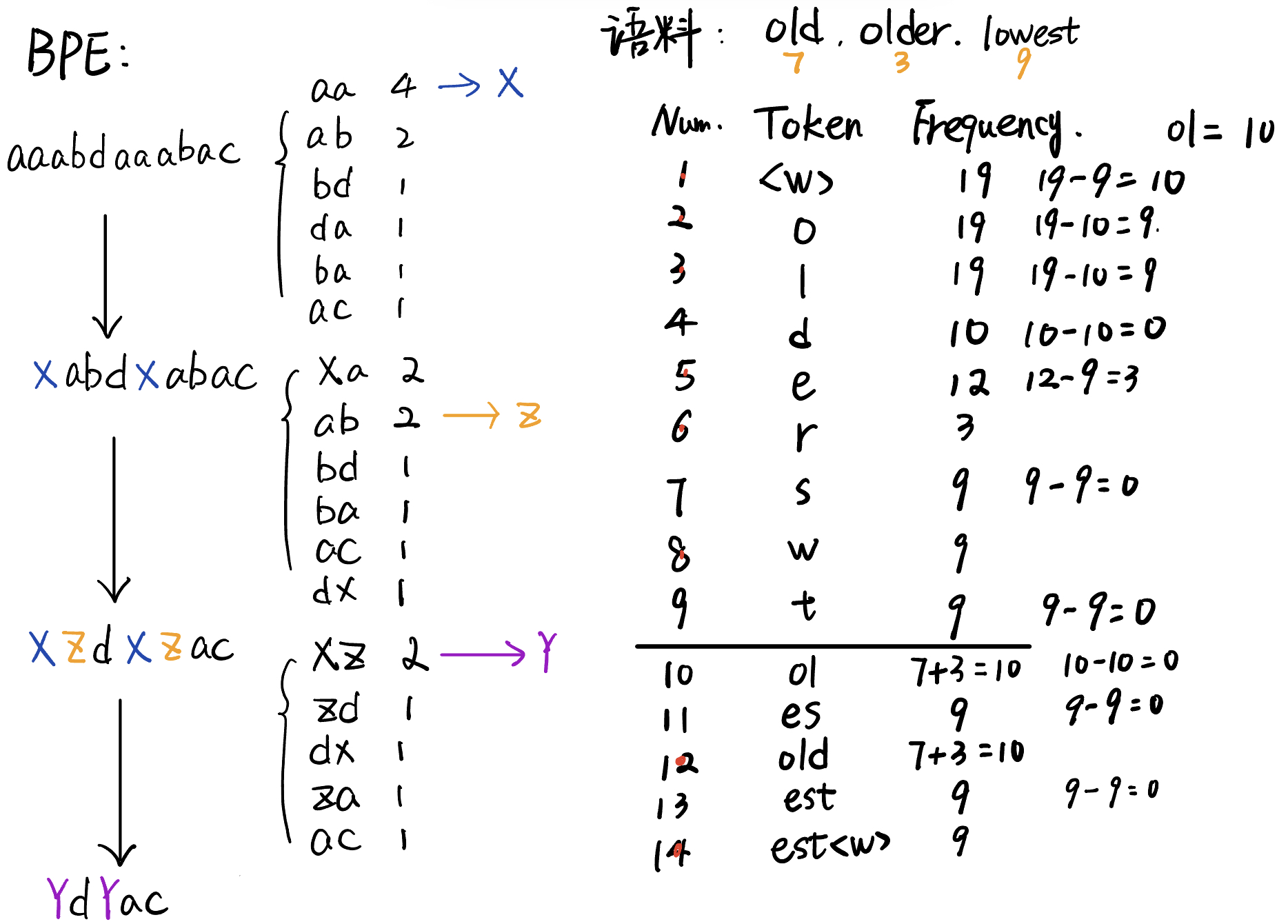
Pytorch and Resource accounting

tensors_memory

Higher precision: more accurate/stable, more memory, more compute

Lower precision: less accurate/stable, less memory, less compute

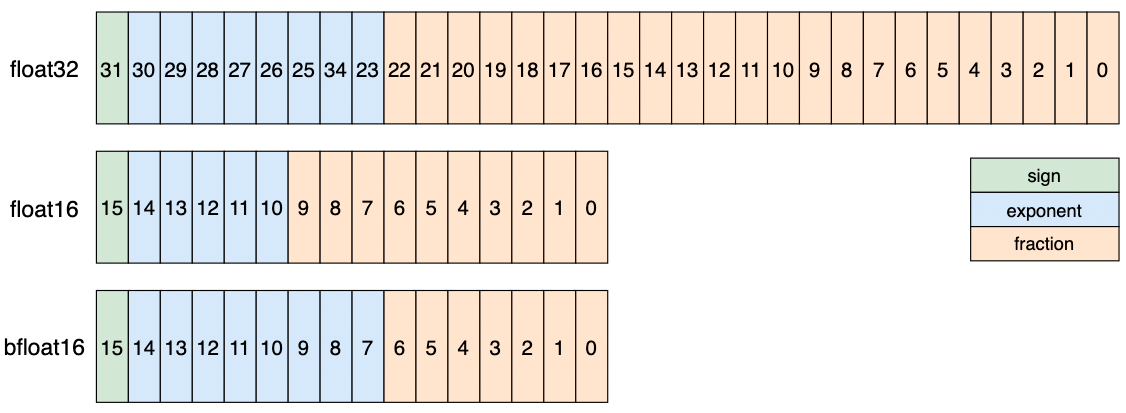
• float32：单精度浮点数是tensor的默认数据类型，4个字节表示一个浮点数。1位符号位， 8位指数位， 23位小数位。神经网络训练时，创建tensor默认的数据类型。

当符号位为0，指数位为11111110，尾数位为全1时，float32的最大值为 $2^{127} \times (1+\frac{2^{23}-1}{2^{23}}=3.40e38$；

当符号位为1，指数位为11111110，尾数位为全1时，float32的最小值为$-2^{127} \times (1+\frac{2^{23}-1}{2^{23}}=-3.40e38$。

• float16：半精度浮点数，两个字节表示一个浮点数。1位符号位， 5位指数位， 10位小数位。相比于float32所占内存更小，但是会出现溢出问题。

当符号位为0，指数位为11110，尾数位为全1时，float16的最大值为 $2^{15} \times (1+\frac{1023}{1024})=65504$；

当符号位为1，指数位为11110，尾数位为全1时，float16的最小值为$-2^{15} \times (1+\frac{1023}{1024}) = -65504$。

• bfloat16：与float16所占内存一致，但是具有float32的存储范围。1位符号位， 8位指数位， 7位小数位。

计算矩阵乘法与前向传播时推荐使用bfloat16数据类型，计算Attention注意力时推荐使用float32数据类型。

指数的偏置：

• float32 的 Bias 为 127
• float16 的 Bias 为 15
• bfloat16 的 Bias 为 127

计算实例如下，以float16为例：

tensors_on_gpus

为了利用好GPUs的并行优势，我们需要将数据从CPU中的RAM移动到GPU中的DRAM中：

if not torch.cuda.is_available():
  return

for i in range(num_gpus):
  properties = torch.cuda.get_device_properties(i)  # @inspect properties
 
y = x.to("cuda:0")
assert x.device == torch.device("cuda",0)

PyTorch中的tensors就是存储在内存中的指针，存储形式如下图所示：

strides[1]表示列指针，strides[0]表示行指针；上图中二维格式为我们习惯上画出的存储格式，但是在内存条中存储的格式本质上是下图中的线性格式。如果要定位一个元素的位置(查找一个元素)，需要利用连个指针进行辅助：$pos=1 * strides[1] + 4 * strides[0]$。

以元素10为例(2行3列)，$pos_{10}=1 * 3 + 4 * 2 = 11$，那么内存中横向第11个位置(从1计数)对应的元素即是10。

tensor_operations

Pytorch对于tensor的操作中，view是free，无须占用内存；但是copy操作(contiguous and reshape)是需要内存开销的。

⚠️einops是之前没有接触过的操作，主要作用是高效操作张量的维度，需要留心学习关注下。推荐一篇博文：https://zhuanlan.zhihu.com/p/342675997

# 矩阵乘法
def tensor_matmul():
  x = torch.ones(16, 32)
  w = torch.ones(32, 2)
  
y = x @ w
assert y.size() == torch.Size([16, 2])

# 定义两个张量:
x: Float[torch.Tensor, "batch seq1 hidden"] = torch.ones(2, 3, 4)  # @inspect x
y: Float[torch.Tensor, "batch seq2 hidden"] = torch.ones(2, 3, 4)  # @inspect y
def tensor_einops():
  #einops主要是rearrange, reduce, repeat这3个方法
  z = x @ y.transpose(-2, -1)  # batch, sequence, sequence  @inspect z --> Old way
  z = einsum(x, y, "batch seq1 hidden, batch seq2 hidden -> batch seq1 seq2")  # @inspect z --> New (einops) way
  z = einsum(x, y, "... seq1 hidden, ... seq2 hidden -> ... seq1 seq2")  # @inspect z
  # reduce
  x: Float[torch.Tensor, "batch seq hidden"] = torch.ones(2, 3, 4)  # @inspect x
  y = x.mean(dim=-1)  # @inspect y --> Old way
  y = reduce(x,"...hidden -> ...","sum") --> New (einops) way
  # rearrange
  x: Float[torch.Tensor, "batch seq total_hidden"] = torch.ones(2, 3, 8)  # @inspect x
  w: Float[torch.Tensor, "hidden1 hidden2"] = torch.ones(4,4)
  
  x = rearrange(x, "... (heads hidden1) -> ... heads hidden1", heads=2)  # @inspect x
  x = einsum(x, w, "... hidden1, hidden1 hidden2 -> ... hidden2")  # @inspect x

Computational cost

LLM里的计算基本上都是浮点运算(FLOP)，类似于加法运算和乘法运算。

容易混淆的概念：

• FLOPs: 浮点运算次数
• FLOP/s：每秒钟浮点计算次数，衡量硬件指标

对 m x n 矩阵进行元素运算需要 O(mn) FLOPs；两个 m x n 矩阵的加法需要 mn 次 FLOPs。一般来说，没有任何运算比矩阵乘法更耗时。

我们用 B 表示数据点的个数，(D K)是参数大小，2 (# tokens) (# parameters)代表前想传播的FLOPs、4 (# data points) (# parameters) 反向传播FLOPs、6 (# data points) (# parameters)代表一次训练的FLOPs。

一个重要指标：Model FLOPs utilization - 模型FLOPs利用率，计算公式如下：

mfu = actual_flop_per_sec / promised_flop_per_sec  # @inspect mfu

FLOP/s取决于硬件(H100 >> A100) 和数据类型(bfloat16 >> float32)。

Parameter initialization

初始化语法：

x = nn.Parameter(torch.randn(input_dim))
w = nn.Parameter(nn.init.trunc_normal_(torch.empty(input_dim, output_dim), std=1 / np.sqrt(input_dim), a=-3, b=3))

维度缩放的原因：为了防止前向传播过程中发生梯度爆炸，导致训练不稳定；将输入进行1/sqrt(input_dim) 缩放，这样每一步都会得到基于正太分布的输出，保证了数据的稳定性。这个道理在注意力机制的计算中同样适用。

⚠️数据加载的注意事项：Don’t want to load the entire data into memory at once！大语言模型的输入是整数序列，可以使用numpy数组加载这些数据，使用memap延迟加载部分数据到内存中。

optimizer的组成：

• momentum = SGD + exponential averaging of grad
• AdaGrad = SGD + averaging by grad$^2$
• RMSProp = AdaGrad + exponentially averaging of grad$^2$
• Adam = RMSProp + momentum